Le puzzle du carré manquant est une illusion d’optique utilisée dans les cours de mathématiques pour aider les élèves à raisonner sur des figures géométriques ; ou plutôt leur apprendre à ne pas raisonner à l’aide de chiffres, mais à n’utiliser que des descriptions textuelles et des axiomes de géométrie.
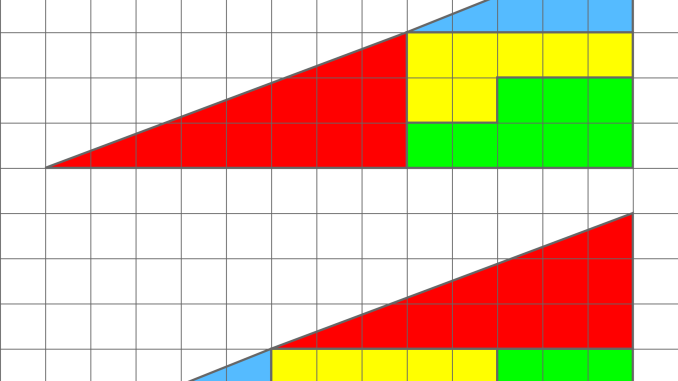
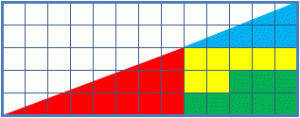
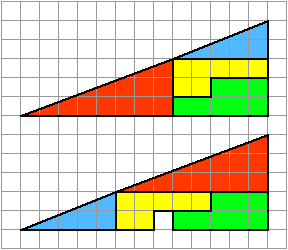
Il représente deux arrangements constitués de formes similaires dans des configurations légèrement différentes. Chacun forme apparemment un triangle rectangle de 13 × 5 , mais l’un d’eux comporte un trou de 1 × 1.
Solution
La clé du puzzle est le fait qu’aucun des « triangles » 13×5 n’est vraiment un triangle, et qu’aucun des deux ne serait vraiment 13×5 s’il l’était, car ce qui semble être l’ hypoténuse est courbé. En d’autres termes, « l’hypoténuse » ne maintient pas une pente constante , même si cela peut apparaître ainsi à l’œil humain.

Un vrai triangle 13×5 ne peut pas être créé à partir des composants donnés. Les quatre figures (les formes jaune, rouge, bleue et verte) totalisent 32 unités de surface. Les triangles apparents formés à partir des figures mesurent 13 unités de largeur et 5 unités de hauteur. Il semble donc que l’aire devrait être S =13×5/2= 32,5 unités. Cependant, le triangle bleu a un rapport de 5:2 (=2,5), tandis que le triangle rouge a un rapport de 8:3 (≈2,667), de sorte que l’ hypoténuse combinée apparente de chaque figure est en réalité courbée. Avec l’hypoténuse courbée, le premier chiffre occupe en réalité un total de 32 unités, tandis que le deuxième chiffre en occupe 33, y compris le carré « manquant ».

Soyez le premier à commenter