في هذا الدرس نتناول المتطابقة الهامة رقم 3 و التي تعرف بجداء صيغتنين مترافقتين ,سنتعرف عليها هندسيا و جبريا و سنقوم بإستخراج القاعدة التي تمكننا من نشر جداء صيغتنين مترافقتين و تعميل مجموع جبري.

التعرف على جداء صيغتنين مترافقتين
تمرين : نريد حساب مساحة شبهي المنحرف التاليين بطريقتين مختلفتين

طريقة 1 : نجمع المساحتين بالكيفية التالية

A = a² – b²
طريقة 2 : أو بالكيفية التالية

(A = (a -b)(a +b
نستنتج إذن أن :a -b)(a +b) = a² – b²)
جبريا : يمكن أن ننشر الجداء (a – b)(a + b):
a² – ab + ba + b² = (a – b)(a + b)
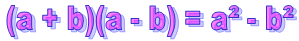
المتساوية a -b)(a +b) = a² – b²) هي متطابقة هامة حيث أن طرفها الأيسر عبارة عن « جداء صيغتنين مترافقتين » و طرفها الأيمن عبارة عن » فرق مربعين« .
- عندما ننتقل من الطرف الأيسر لهذه المتطابقة إلى الطرف الأيمن نقول أننا نشرنا الجداء.
- عندما ننتقل من الطرف الأيمن لهذه المتطابقة إلى الطرف الأيسر نقول أننا عملنا الفرق

Soyez le premier à commenter