المتطابقات الهامة هي متساويات تسهل عملية الحساب والنشر والتعميل، في هذا الدرس نتناول المتطابقة الهامة رقم 1 و التي تعرف بمربع مجموع و سنتعرف عليها هندسيا و جبريا و سنقوم بإستخراج القاعدة التي تمكننا من نشر مربع مجموع و تعميل مجموع جبري.
التعرف على مربع مجموع
تمرين : أحسب بطريقتين مختلفتين مساحة المربع ABCD
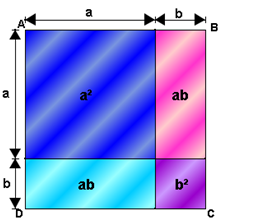 |
| المربع ABCD |
طريقة 1 : نعلم أن مساحة المربع تساوي مربع طول ضلعه
طول ضلع هذا المربع هو a + b, إذن مساحته هي : S(ABCD) = (a + b)²
طريقة 2 : نجزئ المربع إلى مستطيلين و مربعين كما هو مبين في الشكب ثم نحسب مجموع المساحات الجزئية و سيكون لدينا :
نستنتج إذن أن : a + b)² = a² + 2ab + b²)
جبريا : يمكن أن نكتب المربع a + b)²) على شكل (a + b)(a + b) ثم نقوم بعملية النشر المزدوج :

المتساوية a + b)² = a² + 2ab + b²) هي متطابقة هامة حيث أن طرفها الأيسر عبارة عن عن « مربع مجموع » و طرفها الأيمن عبارة عن » مجموع« .
- عندما ننتقل من الطرف الأيسر لهذه المتطابقة إلى الطرف الأيمن ( أي عندما نفكك مربع المجموع إلى مجموع من ثلاثة حدود ) نقول أننا نشرنا المتطابقة.
- عندما ننتقل من الطرف الأيمن لهذه المتطابقة إلى الطرف الأيسر ( أي عندما نجمع المستطيلين و المربعين على شكل مربع مجموع ) نقول أننا عملنا المتطابقة.


Soyez le premier à commenter