لحساب المثلثي او حساب المثلثات هوفرع من فروع الرياضيات يعالج العلاقات بين أضلاع وزوايا المثلثات والخاصيات والتطبيقات العملية للدوال المثلثية كدالة الجيب sinus و جيب تمام cosinus و ظل tangente.
الحساب المثلثي : نبدة تاريخية
وقد كانت أولى التطبيقات العملية للحساب المثلثي في مجالات الملاحة والمساحة والفلك حيث كانت المشكلة الكبرى في كل هذه المجالات تحديد مسافة غير معلومة مثل المسافة بين الأرض و القمر أو مسافة لا يمكن حسابها بصورة مباشرة مثل المسافة التي تغطي بحيرة كبيرة. ومن بين التطبيقات العملية الأخرى لحساب المثلثات استخدام هذا العلم في الفيزياء والكيمياء وكل فروع الهندسة تقريبا خاصة في دراسة الظواهر المتكررة مثل الموجات الصوتية أو تدفق تيار متناوب.
 |
| هيباركوس |
قبل أربعة الف سنة عرف الحساب المثلثي في مصر وبابل، حيث قاس البابليون الزوايا بالدرجات والدقائق والثواني. وحتى عصر اليونانيين، لم يوجد أي تطور ملحوظ في الحساب المثلثي.
وفي القرن الثاني قبل الميلاد، وضع الفلكي هيباركوس جدول مثلثي لحل المثلثات، حيث بدأ بــ 7.5ْ حتى وصل إلى 180ْ بدرجات مقدارها 7.5ْ، وقد أعطى الجدول لكل زاوية طول الوتر المقابل لهذه الزاوية في دائرة ذات شعاع r ثابت . ومثل هذا الجدول مكافئ لجدول الجيب ، ولم تكن القيمة التي استخدمها هيباركوس للشعاع r محددة، ولكن بعد مضي 300 عام استخدم الفلكي بطليموس r = 60 لأن اليونانيين قد أخذوا نظام الأرقام الستينية البابلي.
 |
| بطليموس |
وفي نفس عصر بطليموس تقريبا، طور الهنود نظاما لحساب المثلثات يعتمد على دالة الجيب وليس على دالة الوتر التي اعتمد عليها اليونانيون، وعلى عكس الدالة الحديثة، لم تكن دالة الجيب هذه نسبة وإنما كانت ببساطة طول الضلع المقابل للزاوية في مثلث قائم الزواية ذي وتر ثابت محدد، هذا وقد استخدم الهنود قيما متعددة لوتر المثلث القائم الزاوية.
وفي نهاية القرن الثاني الهجري / الثامن الميلادي، ورث الفلكيون المسلمون التراث اليوناني والهندي واستخدموا دالة الجيب، وبحلول نهاية القرن الرابع الهجري / العاشر الميلادي، كانوا قد أكملوا الجيب والدوال الخمس الأخرى، كما وضعوا العديد من النظريات الأساسية في الحساب المثلثي .
الدائرة المثلثية (تعريف):
معلم متعامد و ممنظم للمستوى :
 |
| شكل 1 : الدائرة المثلثية |
تعريف :
الدائرة المثلثية هي دائرة مركزها O أصل المعلم و شعاعها 1 مزودة بنقطة I و موجهة توجيها موجبا، التوجيه الموجب هو منحى الدوران إنطلاق من في المنحى المضاد لحركة عقارب الساعة (شكل 1).
وحدات قياس الزوايا :
1 – قياس الزاوية بالدرجة :
| |
يمكننا قياس الزاوية بالدرجة و هو القياس الي تعودنا عليه في مرحلة الإعدادي و كما تعلمون هناك زوايا إعتيادية مثل 30 و 60 و 45 و 90 و 180 و 360. الدرجة ليست و حدها وحدة قياس الزوايا و إنما هناك وحدات أخرى كالراديان و الغراد و التي سنتعرف عليها فيما يلي من الفقرتين 2 و 3.
|
2 – قياس الزاوية بالراديان :
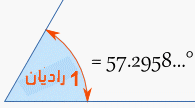
يمكننا أيضا أن نقيس زاوية بالراديان و 1 راديان هو تقريبا 57.2958 بالدرجة :
في دائرة مثلثية لدينا :
 |
| الراديان على الدائرة المثلثية |
يمكنك أن تستنتج أن : π radians = 180°
 |
| π radians = 180° |
قياس زاوية مستقيمية بالدرجة هو °180 أما قياسها بالراديان فهو π و هو طول نصف دائرة شعاعها 1.
إذن: إذا كان قياس زاوية بالدرجة هو °60 فإن قياسها بالراديان هو :
(60 : 180) x π = π/3
بالمثل يمكن أن تجد الزوايا الأخرى ك : °30 و °45 و °90 و … و تحولها إلى الراديان فقط إقسم القياس على 180 و إضرب الناتج في العدد π. و هذا الجدول يلخص هذه الزوايا بالراديان و مقابله بالدرجة :
| القياس بالدرجة |
القياس بالراديان |
| 30° |
π/6 |
| 45° |
π/4 |
| 60° |
π/3 |
| 90° |
π/2 |
| 180° |
π |
| 270° |
3π/2 |
| 360° |
2π |
تعريف :
لتكن C دائرة مركزها O وشعاعها 1 و I و M نقطتين منها. قياس الزاوية الهندسية IOM بالراديان هو الطول a للقوس IM.
يمكنك كذلك أن تستأنس بالبرمجية التالية حتى تتعرف بنفسك على الطول بالراديان في الدائرة المثلثية.
– قياس الزاوية بالغراد :
توجد وحدة أخرى لقياس الزوايا و هي الغراد و قياس زاوية مستقيمية بالغراد هو 200.
إذاكانت x و y و z هي قياسات زاوية هندسية على التوالي ب الدرجة و الراديان و الغراد فإن :
 |
| تناسب وحدات القياس |









Soyez le premier à commenter